Our team will develop fundamental and generalizable computational advances.
Key objectives:
- Develop a computational theory of local-to-global dynamics over multi-scale multi-layer (MSML) networks.
- Develop computational foundations for forecasting, control, and optimization problems in epidemiology.
- Discover fundamental limits to forecasting and inference.
- Develop new statistical and machine learning techniques for ensemble modeling, spatial detection of weak signals, and change detection.
- Explore the use of crowdsourced and active learning methods for inferring individual and community level awareness and behavioral changes.
- Characterize the joint effects of network structure and local interactions on spreading processes.
- Develop HPC-enabled rigorous solutions for scalable validation, calibration, sensitivity analysis, and uncertainty quantification for spreading processes on MSML networks.
Science and Engineering of MSML Networks: We have worked on various problems of analysis, control, and optimization of different kinds of spreading processes on networks arising in epidemiology—this includes the SIS/SIR type processes, as well as complex contagion models.
A fundamental problem in networked epidemiology is designing strategies to control an outbreak. Informally, this involves choosing a subset of nodes/edges to remove, so that the expected number of infections in the residual network is minimized. However, these problems remain generally open, except in the setting of transmission probability of 1 or special classes of graphs (e.g., random graphs). A number of heuristics have been proposed, which choose edges or nodes based on local structural properties, e.g., degree, centrality, and eigenvector components. However, these do not give any guarantees in general, except in very special random graph models. In [1], we develop the first results for this problem when the transmission probability is less than 1. For the edge version of this problem, we give a bicriteria approximation algorithm, which violates the budget and the objective value (the expected number of infections) by constant factors, in the regime in which Karger’s cut sparsification result holds. We consider a larger regime for the transmission probability in the Chung-Lu random graph models, by combining the techniques of sample average approximation and linear programming and rounding. These are the first such results in a rigorous probabilistic model for disease spread.
Vaccine accessibility is one of the factors responsible for lower vaccination coverage in some regions, and so many states have deployed mobile vaccination centers to distribute vaccines across the state. When choosing where to place these sites, there are two important factors to take into account: accessibility and equity. In [2], we formulate a new combinatorial problem that captures these factors and then develop efficient algorithms with theoretical guarantees on both of these aspects. Furthermore, we study the inherent hardness of the problem, and demonstrate strong impossibility results. Finally, we run computational experiments on real-world data to show the efficacy of our methods. We also address demographic equity in the accessibility of vaccine supplies to various sub-populations. This paper was selected as the best student paper at AAMAS 2022.
Our work on designing efficient contact tracing strategies was completed and published during the past year [3]. Contact tracing has proven to be an important strategy to control epidemics during the ongoing COVID-19 pandemic. In this work, we formalize a Markov Decision Process (MDP) framework for the problem of efficient contact tracing that reduces the size of the outbreak while using a limited number of contact tracers. We developed an integer linear programming-based algorithm and showed rigorous bounds on its approximation factor relative to the optimal solution. Its analysis provides insights for a simpler and easily-implementable greedy algorithm based on node degrees. Our computational experiments and simulations on both algorithms on real-world networks show how the algorithms can help in bending the epidemic curve while limiting the number of isolated individuals.
Reinforcement learning studies the problem of making decisions under uncertainty. The usual abstraction is through a Markov decision process where at each step you observe the state and choose an action, which affects the immediate rewards and the transitions to the next state. However, in most applications, especially those related to choosing good policies to control epidemics, we do not have access to full information about the state. This gives rise to a partially observed Markov decision process, or POMDP, where you get an observation whose distribution depends on the hidden state. Most results in POMDPs are negative and in general, there might not even be a succinct description of a good policy in the first place, since it now depends on the entire sequence of observations and actions. In [4], we identify a natural condition where we can get nearly efficient algorithms with strong provable guarantees. The condition we work with is called “observability” and stipulates that the observations leak information about the hidden state. It also gives actionable theory in the sense that in many systems you can choose to deploy more sensors to get additional information, and our work promises that if you can partially observe the hidden state you can guarantee to find a nearly optimal policy. Our paper introduces new techniques for showing linear convergence of the beliefs, giving quantitative bounds for many qualitative results in filtering theory.
Graph cut problems are fundamental in combinatorial optimization and are a central object of study in both theory and practice. A cut can also be viewed as a form of an epidemic intervention, e.g., social distancing involves removing a subset of edges, though this need not be a complete cut, in general. Further, the study of fairness in Algorithmic Design and Machine Learning has recently received significant attention, with many different notions proposed and analyzed for a variety of contexts. In [5], we initiate the study of fairness for graph cut problems by giving the first fair definitions for them, and subsequently, we demonstrate appropriate algorithmic techniques that yield a rigorous theoretical analysis. Specifically, we incorporate two different notions of fairness, namely demographic and probabilistic individual fairness, in a particular cut problem that models disaster containment scenarios. Our results include a variety of approximation algorithms with provable theoretical guarantees.
A more general notion, which is a fundamental unsupervised learning problem, is that of clustering, where a dataset is partitioned into clusters, each consisting of nearby points in a metric space. Clustering has been extended to incorporate fairness constraints in the following manner: each point is associated with a color, representing its group membership, and the objective is that each color has (approximately) equal representation in each cluster to satisfy group fairness. In this model, the cost of the clustering objective increases due to enforcing fairness in the algorithm. The relative increase in the cost, the “price of fairness”, can indeed be unbounded. In [6], we propose to treat an upper bound on the clustering objective as a constraint on the clustering problem and to maximize equality of representation subject to it. We consider two fairness objectives: the group utilitarian objective and the group egalitarian objective, as well as the group leximin objective which generalizes the group egalitarian objective. We derive fundamental lower bounds on the approximation of the utilitarian and egalitarian objectives and introduce algorithms with provable guarantees for them. For the leximin objective, we introduce an effective heuristic algorithm. We further derive impossibility results for other natural fairness objectives.
In [7], we investigate the broadcast problem on 2D grid—this corresponds to a complex transmission process that depends on multiple neighbors—one can think of genetic traits or rumors. The question is: can the source be recovered? More formally, consider a directed acyclic graph with the structure of a 2D regular grid, which has a single source vertex X at layer 0, and k + 1 vertices at distance of k ≥ 1 from X at layer k. Every vertex has outdegree 2, the boundary vertices have indegree 1, and the interior vertices have indegree 2. At time 0, X is given a uniform random bit. At time k ≥ 1, each vertex in layer k receives bits from its parents in layer k − 1, where the bits pass through binary symmetric channels with crossover probability δ ∈ (0,1/2). Each vertex with indegree 2 then combines its input bits with a common Boolean processing function to produce its output bit. The goal is to reconstruct X with probability of error less than 1/2 from all vertices at layer k as k → ∞. Besides their natural interpretation as spread processes, such stochastic processes can be construed as 1D probabilistic cellular automata (PCA) with boundary conditions on the number of sites per layer. Inspired by the “positive rates conjecture” for 1D PCA, we establish that reconstruction of X is impossible for any δ provided that either AND or XOR gates are employed as the common processing function. Furthermore, we show that if certain structured supermartingales exist, reconstruction is impossible for any δ when a common NAND processing function is used. We also provide numerical evidence for the existence of these supermartingales using linear programming.
In [8] we investigate the problem or recovering a random graph from small pieces. More formally, graph shotgun assembly refers to the problem of reconstructing a graph from a collection of local neighborhoods. In this paper, we consider shotgun assembly of Erdös–Rényi random graphs G(n,pn), where pn = n−α for 0 < α < 1. We consider both reconstruction up to isomorphism as well as exact reconstruction (recovering the vertex labels as well as the structure). We show that given the collection of distance-1 neighborhoods, G is exactly reconstructable for 0 < α < 1/3, but not reconstructable for 1/2 < α < 1. Given the collection of distance-2 neighborhoods, G is exactly reconstructable for α ∈ (0, 1/2) ∪ (1/2, 3/5), but not reconstructable for 3/4 < α < 1.
The efficient detection of outbreaks and other cascading phenomena is a fundamental problem in a number of domains, including disease spread, social networks, and infrastructure networks. In such settings, monitoring and testing a small group of pre-selected susceptible population (i.e., sensor set) is often the preferred testing regime—we refer to this as the MinDelSS problem. Prior methods for minimizing the detection time rely on greedy algorithms using submodularity. In [9], we show that this approach can lead to sometimes lead to a worse approximation for minimizing the detection time than desired. We also show that MinDelSS is hard to approximate within an O(n1−1/γ)-factor for any constant γ ≥ 2 (n is the number of nodes in the graph), which motivates our bicriteria approximations. We present with a rigorous worst-case O(log(n))-factor for the detection time, while violating the budget by a factor of O(log2 n). Our algorithm is based on the sample average approximation technique from stochastic optimization, combined with linear programming and rounding. We evaluate our algorithm on several networks, including hospital contact networks, which validates its effectiveness in real settings.
In [10], we define a bridge node to be a node whose neighbor nodes are sparsely connected to each other and are likely to be part of different components if the node is removed from the network. We propose a computationally light neighborhood-based bridge node centrality (NBNC) tuple that could be used to identify the bridge nodes of a network as well as rank the nodes in a network on the basis of their topological position to function as bridge nodes. The NBNC tuple for a node is asynchronously computed on the basis of the neighborhood graph of the node that comprises the neighbors of the node as vertices and the links connecting the neighbors as edges. The NBNC tuple for a node has three entries: the number of components in the neighborhood graph of the node, the algebraic connectivity ratio of the neighborhood graph of the node, and the number of neighbors of the node. We analyze a suite of 60 complex real-world networks and evaluate the computational lightness, effectiveness, efficiency/accuracy, and uniqueness of the NBNC tuple vis-a-vis the existing bridgeness-related centrality metrics and the Louvain community detection algorithm.
Motivated by several recent papers that study algorithmic and complexity aspects of diffusion problems for dynamical systems whose underlying graphs are directed, we investigated several research questions for synchronous dynamical systems on directed acyclic graphs (denoted by DAG-SyDSs). Our initial results were reported in [11]. Subsequently, we developed several additional results on this topic. For example, while the convergence problem for DAG-SyDSs (i.e., given a DAG-SyDs S and an initial configuration C, does S reach a fixed point?) was known to be efficiently solvable, we showed the problem remains computationally intractable for quasi-DAG-SyDSs, where a quasi-DAG is obtained from a DAG by the addition of a single edge. We also showed the reachability problem for DAG-SyDSs is efficiently solvable when each local function is a nested canalyzing function. An extended version of [11] which includes these and other new results have been published [12].
In [13], we consider the simultaneous propagation of two contagions over a social network. We assume a threshold model for the propagation of the two contagions and use the formal framework of discrete dynamical systems. In particular, we study an optimization problem where the goal is to minimize the total number of infections, subject to a budget constraint on the total number of nodes that can be vaccinated. While this problem has been considered in the literature for a single contagion, our work considers the simultaneous propagation of two contagions. We propose a new model for the problem and show that the optimization problem remains NP-hard. We develop a heuristic based on a generalization of the set cover problem. Using experiments on several real-world networks, we compare the performance of the heuristic with some baseline methods. These results show that our heuristic algorithm has very good performance with respect to blocking and can be used even for reasonably large networks. The undergraduate who worked on this project received the 2021 CS Louis T. Rader Undergraduate Research Award.
We say that two configurations of a dynamical system where each node has a state from {0, 1} are similar if the Hamming distance between them is small. Also, a predecessor of a configuration B is a configuration A such that B can be reached in one step from A. In [14], we study problems related to the similarity of predecessor configurations from which two similar configurations can be reached in one time step. We address these problems both analytically and experimentally. Our analytical results point out that the level of similarity between predecessors of two similar configurations depends strongly on the local functions of the dynamical system. Our experimental results considered one class of dynamical systems, namely those with threshold functions. We considered random graphs as well as small world networks. The experimental procedure exploits the fact that the problem of finding predecessors can be reduced to the Boolean Satisfiability problem (SAT). This allows the use of public domain SAT solvers. In general, the experimental results indicate that for large threshold values, as the Hamming distance between a pair of configurations is increased, the average Hamming distance between predecessor sets remains more or less stable. These results suggest that the evolution of trajectories in systems with large thresholds exhibits a certain level of uniformity; that is, similar configurations result from similar predecessors.
Fixed points of a networked dynamical system represent configurations to which the system converges. In the propagation of undesirable contagions (such as rumors and misinformation), convergence to fixed points with a small number of affected nodes is a desirable goal. Motivated by such considerations, we formulated a novel optimization problem of finding a nontrivial fixed point of the system (i.e., a fixed point with at least one affected node) with the minimum number of affected nodes. Our focus was on synchronous dynamical systems where each local function is a threshold function. (For each integer k ≥ 0, the k-threshold Boolean function has the value 1 iff at least k of its inputs have the value 1.) We established that, unless P = NP, there is no polynomial time algorithm for approximating a solution to the nontrivial minimum fixed point problem to within the factor n1−ε for any constant ε > 0. To cope with this computational intractability, we identified several special cases for which the problem can be solved efficiently. Further, we developed an integer linear program that can be used for the problem for networks of reasonable sizes. For solving the problem on larger networks, we proposed a general heuristic framework along with several greedy selection methods. Extensive experimental results on real-world networks demonstrate the effectiveness of the proposed heuristics. These results are reported in [15].
The ongoing COVID-19 pandemic underscores the importance of developing reliable forecasts that would allow decision-makers to devise appropriate response strategies. Despite much recent research on the topic, epidemic forecasting remains poorly understood. Researchers have attributed the difficulty of forecasting contagion dynamics to a multitude of factors, including complex behavioral responses, uncertainty in data, the stochastic nature of the underlying process, and the high sensitivity of the disease parameters to changes in the environment. Our work [16] offers a rigorous explanation of the difficulty of short-term forecasting on networked populations using ideas from computational complexity. Specifically, we show that several forecasting problems (e.g. the probability that at least a given number of people will get infected at a given time and the probability that the number of infections will reach a peak at a given time) are computationally intractable. For instance, efficient solvability of such problems would imply that the number of satisfying assignments of an arbitrary Boolean formula in conjunctive normal form can be computed efficiently, violating a widely believed hypothesis in computational complexity [17]. This intractability result holds even under the ideal situation, where all the disease parameters are known and are assumed to be insensitive to changes in the environment. From a computational complexity viewpoint, our results, which show that contagion dynamics become unpredictable for both macroscopic and individual properties, bring out some fundamental difficulties of predicting disease parameters. We are currently working on the development of efficient algorithms or approximation algorithms for restricted versions of forecasting problems.
We have continued our work on computing network properties with differential privacy. In [18], we study the problem of densest subgraph detection, which is a fundamental graph mining problem, with a large number of applications. There has been a lot of work on efficient algorithms for finding the densest subgraph in massive networks. However, in many domains, the network is private, and returning the densest subgraph can reveal information about the network. Differential privacy is a powerful framework to handle such settings. We study the densest subgraph problem in the edge privacy model, in which the edges of the graph are private. We present the first sequential and parallel differentially private algorithms for this problem. We show that our algorithms give an additive approximation to the multiplicative 1/2-approximation achieved by the greedy peeling algorithm. We evaluate our algorithms on a large number of real-world networks and observe a good privacy-accuracy tradeoff when the network has high density. In ongoing work, we are studying problems of epidemic control under differential privacy.
There are a number of reasons for the fall in immunization rates, but chief among them are concerns about possible side-effects, parents’ own religious and philosophical beliefs, and misperceptions about the risks. It has been observed that peer effects have a significant role in the spread of anti-vaccine sentiment––individuals with such sentiment are in communities with similar sentiment. There is a certain disutility an individual gets by not conforming to their social contacts; on the other hand, the individual gets a utility by conforming to its social contacts. This phenomenon can be viewed as a coordination game, which has been very well studied. In its basic form, the utility of a node in a coordination game is a function of the number of neighbors having the same state as the node.
In our recent work [19], we extend the framework of coordination games and incorporate vaccination decisions–––this requires considering two important components, namely, the benefit a node derives from vaccination and the benefit of herd immunity that all individuals obtain if a large enough fraction of the population is vaccinated. We use Nash equilibria (NE) as the solution concept in such games, and characterize their structure. We show that NE are closely related to the notion of strong communities. We also show a connection between NE and the dynamics of bootstrap percolation, and use it to find the “worst NE”, i.e, the one with the largest number of anti-vaccine nodes. We show that the social optimum (a strategy that maximizes the total utility) can be computed optimally in polynomial time, and derive tight bounds on the Price of Anarchy (the maximum ratio of the total utility of the social optimum and any NE). We study the properties of NE in a diverse class of real-world and social networks and random graphs. We find that there is a threshold value θcritical for the ratio C/α, where C and α are parameters associated with the benefit from vaccination and conformity with neighbors, respectively, such that the number of anti-vaccine nodes in the worst NE shows a dramatic change beyond this threshold.
AI, Theory-Guided Machine Learning, and Massive Data Science: Our team members have worked on a diverse class of problems in this area, both in terms of the foundations as well as applications to problems in epidemiology and related areas.
Multivariate time-series data are gaining popularity in various urban applications, such as emergency management, public health, etc. Segmentation algorithms mostly focus on identifying discrete events with changing phases in such data. For example, consider a power outage scenario during a hurricane. Each time-series can represent the number of power failures in a county for a time period. Segments in such time-series are found in terms of different phases, such as, when a hurricane starts, counties face severe damage, and hurricane ends. Disaster management domain experts typically want to identify the most affected counties (time-series of interests) during these phases. These can be effective for retrospective analysis and decision-making for resource allocation to those regions to lessen the damage. However, getting these actionable counties directly (either by simple visualization or looking into the segmentation algorithm) is typically hard. In [1], we introduce and formalize a novel problem RaTSS (Rationalization for time-series segmentation) that aims to find such time-series (rationalizations), which are actionable for the segmentation. We also propose an algorithm Find-RaTSS to find them for any black-box segmentation. We show Find-RaTSS outperforms non-trivial baselines on generalized synthetic and real data, also provides actionable insights in multiple urban domains, especially disasters and public health.
For real-time forecasting in domains like public health and macroeconomics, data collection is a non-trivial and demanding task. Often after being initially released, it undergoes several revisions later (maybe due to human or technical constraints). As a result, it may take weeks until the data reaches a stable value. This so-called “backfill” phenomenon and its effect on model performance have been barely addressed in the prior literature. In [2], we introduce the multi-variate backfill problem using COVID-19 as the motivating example. We construct a detailed dataset composed of relevant signals over the past year of the pandemic. We then systematically characterize several patterns in backfill dynamics and leverage our observations for formulating a novel problem and neural framework, Back2Future, that aims to refine a given model’s predictions in real-time. Our extensive experiments demonstrate that our method refines the performance of a diverse set of top models for COVID-19 forecasting and GDP growth forecasting. Specifically, we show that Back2Future refined top COVID-19 models by 6.65% to 11.24% and yielded 18% improvement over non-trivial baselines. In addition, we show that our model improves model evaluation too; hence policy-makers can better understand the true accuracy of forecasting models in real-time. In addition, we show that our model improves model evaluation too; hence policy-makers can better understand the true accuracy of forecasting models in real-time.
Probabilistic hierarchical time-series forecasting is an important variant of time-series forecasting, where the goal is to model and forecast multivariate time-series that have underlying hierarchical relations. Most methods focus on point predictions and do not provide well-calibrated probabilistic forecast distributions. Recent state-of-art probabilistic forecasting methods also impose hierarchical relations on point predictions and samples of distribution which do not account for the coherency of forecast distributions. Previous works also silently assume that datasets are always consistent with given hierarchical relations and do not adapt to real-world datasets that show deviation from this assumption. In ongoing work, the Georgia Tech team closes both these gaps and proposes PROFHiT, which is a fully probabilistic hierarchical forecasting model that jointly models forecast distribution of the entire hierarchy. PROFHiT uses a flexible probabilistic Bayesian approach and introduces a novel Distributional Coherency regularization to learn from hierarchical relations for entire forecast distribution that enables robust and calibrated forecasts as well as adapt to datasets of varying hierarchical consistency. On evaluating PROFHiT over a wide range of datasets, we observed 41-88% better performance in accuracy and calibration. Due to modeling the coherency over full distribution, we observed that PROFHiT can robustly provide reliable forecasts even if up to 10% of input time-series data is missing whereas other methods’ performance severely degrades by over 70%.
As AI is increasingly supporting human decision-making, there is more emphasis than ever on building trustworthy AI systems. Despite the discrepancies in terminology, almost all recent research on trustworthy AI agrees on the need for building AI models that produce consistently correct outputs for the same input. Although this seems like a straightforward requirement, as we periodically retrain AI models in the field there is no guarantee that different generations of the model will be consistently correct when presented with the same input. Consider the damage that can be caused by an AI agent for COVID-19 diagnosis that correctly recommends a true patient to self-isolate, then changes its recommendation after being retrained with more data. Producing consistent outputs by deep learning models is crucial for all domains including epidemic forecasting. In [3], we introduce a new concept of learning models—consistency. We define consistency as the ability of a model to reproduce an output for the same input after retraining, irrespective of whether the outputs are correct/incorrect, and define correct-consistency as the ability of the model to reproduce a correct output for the same input. We provide a theoretical explanation of why and how ensemble learning can improve consistency and correct-consistency. We also prove that adding components with accuracy higher than the average accuracy of ensemble component learners to an ensemble learner can yield a better consistency for correct predictions. Based on these theoretical findings, we propose a dynamic snapshot ensemble with a pruning algorithm to boost predictive correct-consistency and accuracy in an efficient way. We examined the proposed theorems and method using multiple text and image datasets for classification. The proposed method has boosted the state-of-the-art performance. The results demonstrated the effectiveness and efficiency of the proposed ensemble method and prove the theorems empirically.
In [4–7], we present the study of technologies to support deep learning with an emphasis on the efficient linking of C++, Java, and Python modules. In [8],
we present the study of a privacy-preserving SGX-based Big Data framework on human genome analytics. In terms of applications, [9] shows approaches to surrogates for COVID computational biology simulations addressing the large computational bottleneck in solving the diffusion equation. Our study of deep learning for time series that started with work on COVID-19 data [10, 11] extended to other areas (hydrology and earthquake) with the identification of spatial time [4] series that are very common and important. This research looked at recurrent and transformer neural net architectures.
In [12], we introduce a new class of physics-informed neural networks-named Epidemiologically-Informed Neural Networks (EINNs)-crafted for epidemic forecasting. We investigate how to leverage both the theoretical flexibility provided by mechanistic models as well as the data-driven expressibility afforded by AI models, to ingest heterogeneous information. Although neural forecasting models have been successful in multiple tasks, long-term predictions and anticipating trend changes remain open challenges. Epidemiological ODE (Ordinary Differential Equations) models contain mechanisms that can guide us in these two tasks; however, they have limited capability of ingesting data sources and modeling composite signals. Thus, we propose to supervise neural networks with epidemic mechanistic models while simultaneously learning their hidden dynamics. Our method allows neural models to have the flexibility to learn the disease spread dynamics and use auxiliary features in a general framework. In contrast with previous work, we do not assume the observability of complete dynamics and do not need to numerically solve the ODE equations during training. Our results showcase that our method can indeed leverage the "best of both worlds" compared to other non-trivial ways of merging such approaches.
It was critical to get data about the COVID-19 spread in the US in the early days of the epidemic. Beginning in April 2020, we gathered partial county-level data on non-pharmaceutical interventions (NPIs) implemented in response to the COVID-19 pandemic in the United States, using both volunteer and paid crowdsourcing. We prepared a report, documenting the data collection process and summarizing our results, to increase the utility of our open data and inform the design of future rapid crowdsourcing data collection efforts [13].
Countering Misinformation. Some of the major challenges with current epidemiological situations are social in nature, with rumors and misinformation spreading faster than best practices, science, or vaccines can keep up. It is thus critical to investigate approaches that maintain productive and open discussions on online social platforms. To address this problem, we studied how the group-chatting platform Discord coordinated with experienced volunteer moderators to respond to hate and harassment toward LGBTQ+ communities during Pride Month, June 2021, in what came to be known as the “Pride Mod” initiative. Representatives from Discord and volunteer moderators collaboratively identified and communicated with targeted communities, and volunteers temporarily joined servers that requested support to supplement those servers’ existing volunteer moderation teams. Though LGBTQ+ communities were subject to a wave of targeted hate during Pride Month, the communities that received the requested volunteer support reported having a better capacity to handle the issues that arose. We reported the results of interviews with 11 moderators who participated in the initiative as well as the Discord employee who coordinated it. We showed how this initiative was made possible by the way Discord has cultivated trust and built formal connections with its most active volunteers, and discussed the ethical implications of formal collaborations between for-profit platforms and volunteer users [14].
A key challenge in biomedical data is that our knowledge of biological systems is limited and that many aspects of their structure and function are unknown. It is thus critical for the methods to be applicable in open-world scenarios. A fundamental limitation of applying semi-supervised learning in such real-world settings is the assumption that unlabeled test data contains only classes previously encountered in the labeled training data. However, this assumption rarely holds for data in-the-wild, where instances belonging to novel classes may appear at testing time. We developed a novel open-world semi-supervised learning setting that formalizes the notion that novel classes may appear in the unlabeled test data. In this novel setting, the goal is to solve the class distribution mismatch between labeled and unlabeled data, where at the test time every input instance either needs to be classified into one of the existing classes or a new unseen class needs to be initialized. To tackle this challenging problem, we proposed ORCA, an end-to-end deep learning approach that introduces uncertainty adaptive margin mechanism to circumvent the bias towards seen classes caused by learning discriminative features for seen classes faster than for the novel classes. In this way, ORCA reduces the gap between intra-class variance of seen classes with respect to novel classes. Experiments on image classification datasets and a single-cell annotation dataset demonstrate that ORCA consistently outperforms alternative baselines, achieving 25% improvement on seen and 96% improvement on novel classes of the ImageNet dataset. This work was accepted at ICLR’22 [15].
AI is undergoing a paradigm shift with the rise of models (e.g., BERT, DALL-E, GPT-3), called foundation models, that are trained on broad data at scale and are adaptable to a wide range of downstream tasks. We participated in a report that provides a thorough account of the opportunities and risks of foundation models, ranging from their capabilities (e.g., language, vision, robotics, reasoning, human interaction) and technical principles(e.g., model architectures, training procedures, data, systems, security, evaluation, theory) to their applications (e.g., law, healthcare, education) and societal impact (e.g., inequity, misuse, economic and environmental impact, legal and ethical considerations). In particular, our contribution to the report was in describing current examples of foundation models in healthcare and biomedicine and their already significant impact on diverse areas in biomedicine [16].
The main paradigm for modeling agents in computer science is the Belief-Desire-Intention (BDI) paradigm. In this approach, an agent has one or more desires (goals), which it tries to achieve by making a plan (intentions) based on its beliefs about the world. Over the last two decades, sophisticated agent-oriented programming frameworks have been developed to support BDI modeling, however integrating these with large-scaled agent-based simulations has been a challenge. We have developed a system that combines an agent-oriented programming framework called Sim-2APL, along with a new HPC simulator called PanSim to allow large-scale distributed epidemic simulations with BDI agents. Experiments with a synthetic population of Virginia (~8 million agents) show weak and strong scaling [17]. Our simulation of COVID-19, built using this framework, focuses on the early stage of the epidemic (Mar - Jun 2020). Using a synthetic population of Virginia, we calibrated the simulation to both COVID case data and mobility data from Cuebiq using Bayesian Optimization. We then used it to evaluate the efficacy of the various Executive Orders that were put in place in Virginia during that time period [18].
In recently completed work [19], we demonstrated the successful use of federated learning in a diverse set of data analytics problems in healthcare and epidemiology. Specifically, we reproduce eight diverse health studies in terms of study design, statistical analysis, and sample size, spanning the past several decades in a purely federated setting, where each unit of federation keeps its data private but still contributes to the aggregate model. These studies represent a gamut of study designs (four cohort studies, three case series, one clinical trial), statistical tasks (three prediction tasks in terms of AUROC, five inference tasks in terms of relative risks) and sample sizes (Range, 159–53,423). We find that the results from federated learning are on par with centralized models, both in terms of performance (AUC) and interpretation (measured as odds ratio or coefficient). We also show that new methods involving federated learning and differential privacy can provide very strong privacy protections with minimal reduction in utility, with ε being a small constant, and δ < 10−5.
To control the pandemic, mass testing is one of the essential methods to bring healthy individuals back to regular social activities and promptly treat potential asymptomatic infected individuals. However, the testing capacity for infectious diseases such as COVID-19 is still too scarce to meet global health needs. Testing strategies are urgently needed for quickly identifying the infected individuals within the community to control the disease transmission. Since the contact network provides social contact information and potential reliance on disease transmission, in ongoing work, we propose a graph partition-based group testing strategy to address the mass testing challenges. Our goal is to minimize the expected number of tests to screen the entire contact network. The testing strategy can automatically partition the contact network into a certain number of balanced subgraphs and determine the risk level based on the residents’ social contact characteristics. A testing order will be assigned to each sub-graph according to its risk level and the testing capacity. We will introduce an improved infectious disease transmission model to simulate the virus’s dynamic spread. We are working on first building an improved compartmental model to capture the superspreading characteristics in the COVID-19 pandemic based on the classic SEIR model and simulate the virus transmission in the contact network. Next, we will develop a risk model that takes advantage of the previous test results and the social contact activity to estimate the potentially infected percentage of the resident group. We will construct an adaptive dynamic group testing strategy based on the model to minimize the expected number of tests needed to screen the entire network while minimizing the number of newly infected cases simultaneously. We are also working on evaluating the selected social activity feature based on the proposed machine learning model to give insights for future pandemic preventive and control measures.
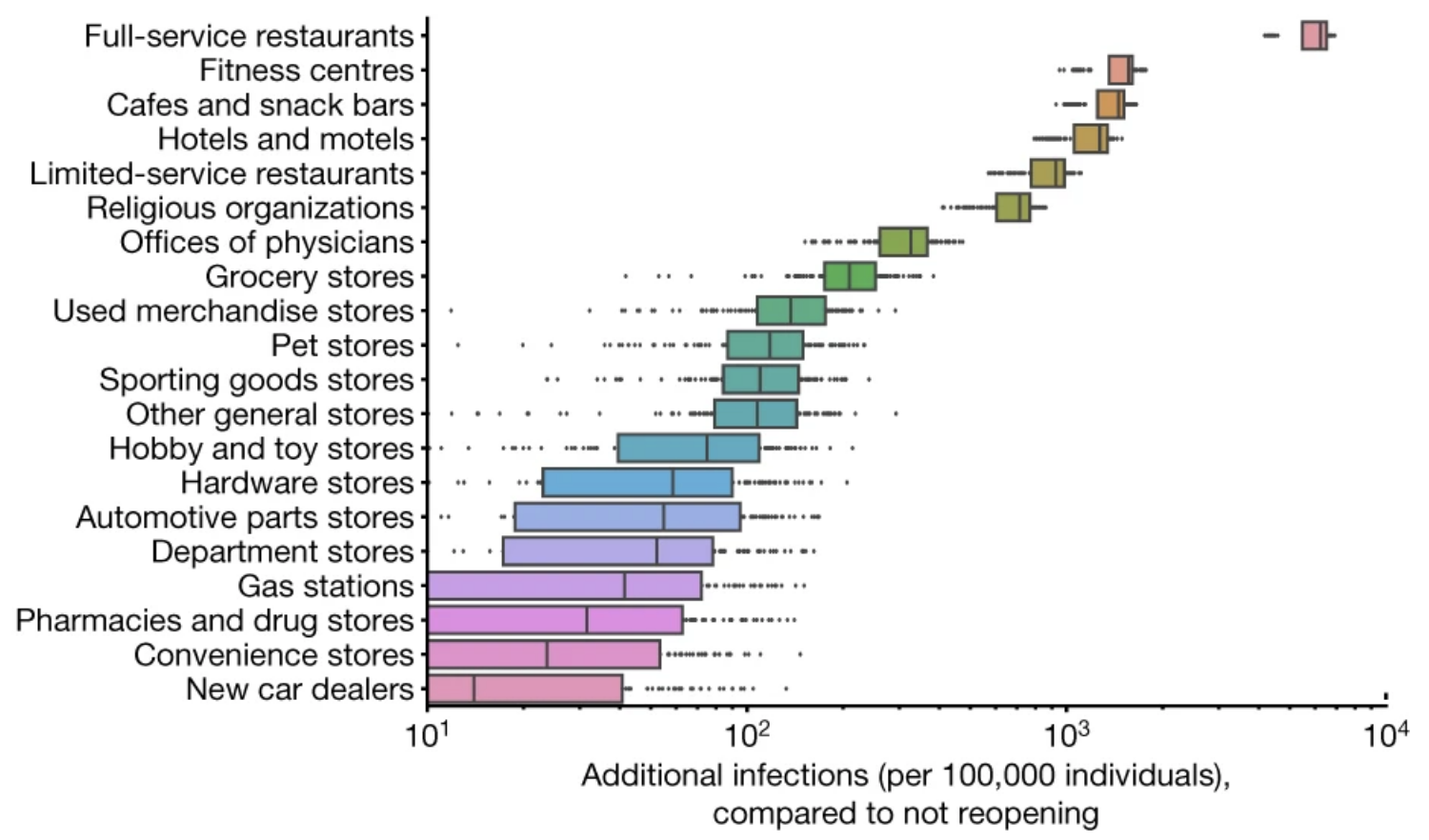 The COVID-19 pandemic dramatically changed human mobility patterns, necessitating epidemiological models which capture the effects of changes in mobility on virus spread. We developed a novel metapopulation SEIR model, published in Nature [20], that integrates fine-grained, dynamic mobility networks to simulate the spread of SARS-CoV-2 in 10 of the largest US metropolitan statistical areas. Derived from cell phone data, our mobility networks map the hourly movements of 98 million people from neighborhoods (census block groups, or CBGs) to points of interest (POIs) such as restaurants and religious establishments, connecting 57k CBGs to 553k POIs with 5.4 billion hourly edges. We showed that by integrating these networks our model can accurately fit the real case trajectory, despite substantial changes in population behavior over time. Our model indicates that a small minority of “superspreader” POIs account for a large majority of infections and that restricting maximum occupancy at each POI is more effective than uniformly reducing mobility. Our model also correctly predicts higher infection rates among disadvantaged racial and socioeconomic groups solely from differences in mobility: we found that disadvantaged groups have not been able to reduce mobility as sharply and that the POIs they visit are more crowded and therefore higher risk. By capturing who is infected at which locations, our model supports detailed analyses that can inform more effective and equitable policy responses to COVID-19. Building on and further refining the model above, we collaborated with the Virginia Department of Health on a decision-support tool that utilizes large-scale data and epidemiological modeling to quantify the impact of changes in mobility on infection rates. To balance these competing demands, policymakers need analytical tools to assess the costs and benefits of different mobility reduction measures. Our model captures the spread of COVID-19 by using a fine-grained, dynamic mobility network that encodes the hourly movements of people from neighborhoods to individual places, with over 3 billion hourly edges. By perturbing the mobility network, we can simulate a wide variety of reopening plans and forecast their impact in terms of new infections and the loss in visits per sector. To deploy this model in practice, we built a robust computational infrastructure to support running millions of model realizations, and we worked with policymakers to develop an intuitive dashboard interface that communicates our model’s predictions for thousands of potential policies, tailored to their jurisdiction. The resulting decision-support environment provides policymakers with much-needed analytical machinery to assess the trade-offs between future infections and mobility restrictions.
The COVID-19 pandemic dramatically changed human mobility patterns, necessitating epidemiological models which capture the effects of changes in mobility on virus spread. We developed a novel metapopulation SEIR model, published in Nature [20], that integrates fine-grained, dynamic mobility networks to simulate the spread of SARS-CoV-2 in 10 of the largest US metropolitan statistical areas. Derived from cell phone data, our mobility networks map the hourly movements of 98 million people from neighborhoods (census block groups, or CBGs) to points of interest (POIs) such as restaurants and religious establishments, connecting 57k CBGs to 553k POIs with 5.4 billion hourly edges. We showed that by integrating these networks our model can accurately fit the real case trajectory, despite substantial changes in population behavior over time. Our model indicates that a small minority of “superspreader” POIs account for a large majority of infections and that restricting maximum occupancy at each POI is more effective than uniformly reducing mobility. Our model also correctly predicts higher infection rates among disadvantaged racial and socioeconomic groups solely from differences in mobility: we found that disadvantaged groups have not been able to reduce mobility as sharply and that the POIs they visit are more crowded and therefore higher risk. By capturing who is infected at which locations, our model supports detailed analyses that can inform more effective and equitable policy responses to COVID-19. Building on and further refining the model above, we collaborated with the Virginia Department of Health on a decision-support tool that utilizes large-scale data and epidemiological modeling to quantify the impact of changes in mobility on infection rates. To balance these competing demands, policymakers need analytical tools to assess the costs and benefits of different mobility reduction measures. Our model captures the spread of COVID-19 by using a fine-grained, dynamic mobility network that encodes the hourly movements of people from neighborhoods to individual places, with over 3 billion hourly edges. By perturbing the mobility network, we can simulate a wide variety of reopening plans and forecast their impact in terms of new infections and the loss in visits per sector. To deploy this model in practice, we built a robust computational infrastructure to support running millions of model realizations, and we worked with policymakers to develop an intuitive dashboard interface that communicates our model’s predictions for thousands of potential policies, tailored to their jurisdiction. The resulting decision-support environment provides policymakers with much-needed analytical machinery to assess the trade-offs between future infections and mobility restrictions.
High-resolution mobility datasets have become increasingly available in the past few years and have enabled detailed models for infectious disease spread including those for COVID-19. However, there are open questions on how such mobility data can be used effectively within epidemic models and for which tasks they are best suited. In this work, we extract a number of graph-based proximity metrics from high-resolution cellphone trace data from X-Mode and use it to study COVID-19 epidemic spread in 50 land grant university counties in the US. We present an approach to estimating the effect of mobility on cases by fitting an ordinary differential equation-based model and performing multivariate linear regression to explain the estimated time-varying transmissibility. We find that, while mobility plays a significant role, the contribution is heterogeneous across the counties, as exemplified by a subsequent correlation analysis. We also evaluate the metrics’ utility for case surge prediction defined as a supervised classification problem and show that the learned model can predict surges with 95% accuracy and 87% F1-score [21].
The COVID-19 pandemic demonstrated the need for accelerated drug discovery pipelines. We have been developing novel machine learning-based approaches for this problem. Our work covers: (i) identification of disease treatment mechanisms, (ii) a machine learning platform for evaluating therapeutics, and (iii) improving drug safety. Most diseases disrupt multiple proteins, and drugs treat such diseases by restoring the functions of the disrupted proteins. How drugs restore these functions, however, is often unknown as a drug’s therapeutic effects are not limited only to the proteins that the drug directly targets. We developed the multiscale interactome, a powerful approach to explaining disease treatment [22]. We integrated disease-perturbed proteins, drug targets, and biological functions into a multiscale interactome network, which contains 478,728 interactions between 1,661 drugs, 840 diseases, 17,660 human proteins, and 9,798 biological functions. We found that a drug’s effectiveness can often be attributed to targeting proteins that are distinct from disease-associated proteins but that affect the same biological functions. We developed a random walk-based method that captures how drug effects propagate through a hierarchy of biological functions and are coordinated by the protein-protein interaction network in which drugs act. On three key pharmacological tasks, we found that the multiscale interactome predicts what drugs will treat a given disease more effectively than prior approaches, identifies proteins and biological functions related to treatment, and predicts genes that interfere with treatment to alter drug efficacy and cause serious adverse reactions. Our results indicate that physical interactions between proteins alone are unable to explain the therapeutic effects of drugs as many drugs treat diseases by affecting the same biological functions disrupted by the disease rather than directly targeting disease proteins or their regulators. Our general framework allows for identification of proteins and biological functions relevant to treatment, even when drugs seem unrelated to the diseases they are recommended for. Machine learning for therapeutics is an emerging field with incredible opportunities for innovation and expansion. We introduced Therapeutics Data Commons (TDC), the first unifying framework to systematically access and evaluate machine learning across the entire range of therapeutics [23, 24]. At its core, TDC is a collection of curated datasets and learning tasks that can translate algorithmic innovation into biomedical and clinical implementation. To date, TDC includes 66 machine learning-ready datasets from 22 learning tasks, spanning the discovery and development of safe and effective medicines. TDC also provides an ecosystem of tools, libraries, leaderboards, and community resources, including data functions, strategies for systematic model evaluation, meaningful data splits, data processors, and molecule generation oracles. All datasets and learning tasks are integrated and accessible via an open-source library. We envision that TDC can facilitate algorithmic and scientific advances and accelerate development, validation, and transition into production and clinical implementation. TDC is a continuous, open-source initiative, and we invite contributions from the research community. TDC is publicly available at https://tdcommons.ai. Improving drug safety is critical to mitigating the health burden of infectious diseases. Approximately 1 in 3 novel therapeutics approved by the FDA is associated with a severe post-market safety event, where new safety risks are identified after the initial regulatory approval. Understanding the root causes of these post-market safety events can inform clinical trial design and regulatory decision-making, which will ultimately improve drug safety. Using a dataset of 10,443,476 reports across 3,624 drugs and 19,193 adverse events, we have started to explore the relationship between post-market safety events and the diversity of subject population in pre-market clinical trials across race, gender, age, and geography. Our initial findings in this ongoing study indicate that the racial representativeness of pre-market clinical trials is strongly associated with post-market safety events and that there is a negative association between international clinical trial sites and safety.
Can we infer all the failed components of an infrastructure network, given a sample of reachable nodes from supply nodes? One of the most critical post-disruption processes after a natural disaster is to quickly determine the damage or failure states of critical infrastructure components. However, this is non-trivial considering that often only a fraction of components may be accessible or observable after a disruptive event. Past work has looked into inferring failed components given point probes, i.e. with a direct sample of failed components. In contrast, we study the harder problem of inferring failed components given partial information of some ‘serviceable’ reachable nodes and a small sample of point probes, being the first often more practical to obtain. We formulate this novel problem using the Minimum Description Length (MDL) principle and then present a greedy algorithm that minimizes MDL cost-effectively. We evaluate our algorithm on domain-expert simulations of real networks in the aftermath of an earthquake. Our algorithm successfully identifies failed components, especially the critical ones affecting overall system performance. This work has been published in [25] (full version); a preliminary version appeared as [26].
Calibration, validation and uncertainty quantification
Accurate and trustworthy epidemic forecasting is an important problem for public health planning and disease mitigation. Most existing epidemic forecasting models disregard uncertainty quantification, resulting in mis-calibrated predictions. Recent works in deep neural models for uncertainty-aware time-series forecasting also have several limitations; e.g., it is difficult to specify proper priors in Bayesian NNs, while methods like deep ensembling can be computationally expensive. In [1], we propose to use neural functional processes to fill this gap. We model epidemic time-series with a probabilistic generative process and propose a functional neural process model called EpiFNP, which directly models the probability distribution of the forecast value in a non-parametric way. In EpiFNP, we use a dynamic stochastic correlation graph to model the correlations between sequences, and design different stochastic latent variables to capture functional uncertainty from different perspectives. Our experiments in a real-time flu forecasting setting show that EpiFNP significantly outperforms state-of-the-art models in both accuracy and calibration metrics, up to 2.5x in accuracy and 2.4x in calibration. Additionally, as EpiFNP learns the relations between the current season and similar patterns of historical seasons, it enables interpretable forecasts. Beyond epidemic forecasting, EpiFNP can be of independent interest for advancing uncertainty quantification in deep sequential models for predictive analytics.
Probabilistic time-series forecasting enables reliable decision-making across many domains. Most forecasting problems have diverse sources of data containing multiple modalities and structures. Leveraging information as well as uncertainty from these data sources for well-calibrated and accurate forecasts is an important challenging problem. Most previous work on multi-modal learning and forecasting simply aggregate intermediate representations from each data view by simple methods of summation or concatenation and does not explicitly model uncertainty for each data-view. In [2], we proposed a general probabilistic multi-view forecasting framework, CAMul, that can learn representations and uncertainty from diverse data sources. It integrates the knowledge and uncertainty from each data view in a dynamic context-specific manner assigning more importance to useful views to model a well-calibrated forecast distribution. We use CAMul for multiple domains with varied sources and modalities and show that CAMul outperforms other state-of-art probabilistic forecasting models by over 25% in accuracy and calibration.
We have worked on diverse uncertainty quantification (UQ) problems in epidemiology and related domains. In [3], we headed a collaborative effort to produce a review paper on the emulation of stochastic computer models. We are also exploring Bayesian approaches to more effectively characterize uncertainty in population reconstructions based on a variety of different data sources. We developed a Bayesian auxiliary variable model for analyzing data with both continuous and discrete outcomes from epidemiological studies, which led to the publication of [4]. As data with mixed outcomes are widely observed in epidemiological studies, we further developed a generative approach to modeling data with quantitative and qualitative responses [5]. In this research work, we propose a novel generative approach to jointly model the QQ responses by incorporating the dependency information of predictors. The proposed method is computationally efficient and provides accurate parameter estimation under a penalized likelihood framework. Moreover, because of the generative approach framework, the asymptotically theoretical results of the proposed method are established under some regularity conditions.


